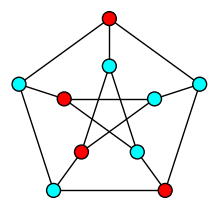
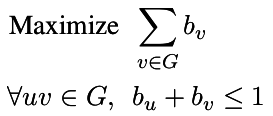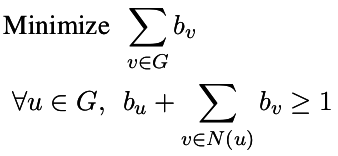| Independent Set |
| Maximum set of pairwise non-adjacent vertices in a graph |
 |
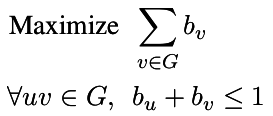 |
p = MixedIntegerLinearProgram(maximization = True)
b = p.new_variable(binary = True)
p.set_objective( sum([b[v] for v in g]) )
for u,v in g.edges(labels = False):
p.add_constraint( b[u] + b[v] <= 1 )
p.solve()
b = p.get_values(b)
print [v for v,i in b.items() if i]
# Note: viewed as a boolean, 0 is False and 1.0 is True
|
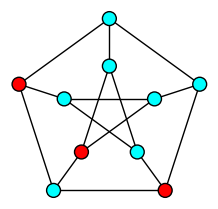
| Dominating Set |
| Minimum set of vertices whose neighborhood is the whole graph |
 |
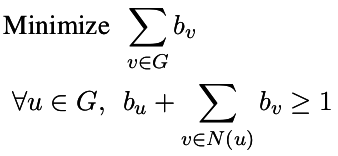 |
|
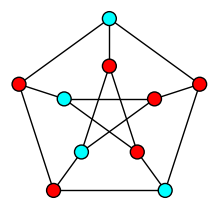
| Vertex Cover |
| Minimum Set of vertices touching each edge |
 |
|
|
| Partition |
| Partition a set of integers into two sets whose sum is equal |
 |
|
|
| Bipartite Set |
| Partition the graph into two independent sets |
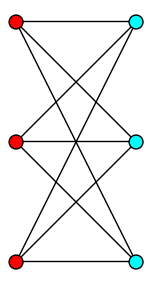 |
|
|
| Subset Sum |
| Find a nonempty subset of integers with null sum |
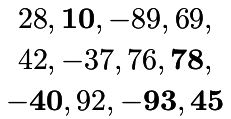 |
|
|
| Distances |
| Compute the distance from vertex 0 to any other |
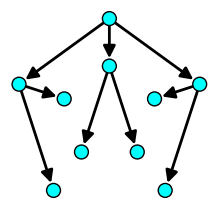 |
|
|
| Girth |
| Size of the shortest cycle |
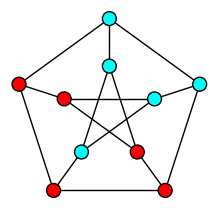 |
|
|
| Matching |
| Maximum number of non-incident edges |
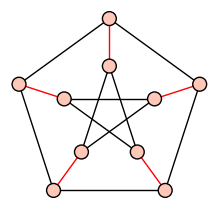 |
|
|
| Feedback Arc Set |
| Minimum set of arcs hitting all circuits |
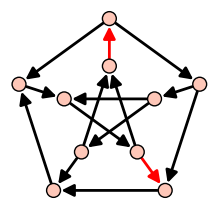 |
|
|
| Feedback Vertex Set |
| Minimum set of vertices hitting all circuits |
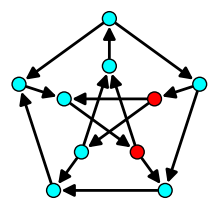 |
|
|
| Hamiltonian Cycle |
| A cycle going through all vertices |
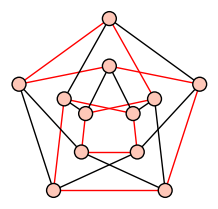 |
|
|
| 3-coloration |
| Partition a graph into three independent sets |
 |
|
|
| GCD |
| The gcd of a list of integers |
gcd([12,15,30]) = 3 |
|
|
| Sudoku |
| Fill an incomplete Sudoku grid |
Get some instances of the Sudoku class and solve them, for example:
sage: S = Sudoku('\
....: 1....7.9.\
....: .3..2...8\
....: ..96..5..\
....: ..53..9..\
....: .1..8...2\
....: 6....4...\
....: 3......1.\
....: .4......7\
....: ..7...3..') ; S
+-----+-----+-----+
|1 | 7| 9 |
| 3 | 2 | 8|
| 9|6 |5 |
+-----+-----+-----+
| 5|3 |9 |
| 1 | 8 | 2|
|6 | 4| |
+-----+-----+-----+
|3 | | 1 |
| 4 | | 7|
| 7| |3 |
+-----+-----+-----+
sage: sudoku_solve_milp(S)
+-----+-----+-----+
|1 6 2|8 5 7|4 9 3|
|5 3 4|1 2 9|6 7 8|
|7 8 9|6 4 3|5 2 1|
+-----+-----+-----+
|4 7 5|3 1 2|9 8 6|
|9 1 3|5 8 6|7 4 2|
|6 2 8|7 9 4|1 3 5|
+-----+-----+-----+
|3 5 6|4 7 8|2 1 9|
|2 4 1|9 3 5|8 6 7|
|8 9 7|2 6 1|3 5 4|
+-----+-----+-----+
|
|
|